1. 課題を見つける／仮説を立てる

2. 実験や観察をしてデータを集める

3. データを整理する

4. データを解析して仮説を検証する

• 仮説の検証にはエビデンスが必要
• でも生物の表現型には ばらつきがある
• 実験や観察で得られた差や効果は偶然の産物じゃないの？
  • これに答えるのが統計解析
  • 推論や予測などにも使うよ

• 実験生物学でよく使う超古典的 + 基本的な統計解析法
  • 統計解析にあたっての心構え
  • 各解析方法の実践（理論についてはほぼやりません！）
• Rのみ（有料ソフトなし）ででき、発展的な解析の足がかりへ

統計的仮説検定…“有意差”を求める超古典的な群間比較

1. 仮説検定の進め方（正規性, 等分散性の検定など）
2. ２群の検定（Studentのt検定など）
3. 多群の検定（ANOVAなど）

統計モデリング…値の関係性を調べる

1. 一般線形モデル（lm）
2. 一般化線形モデル（glm）

統計解析…標本に基づいて、母集団の性質を推定する

• 母集団の性質を知りたいが実測は不可能
• そこでランダムに抽出した標本から母集団の性質を推定する
  • 実験で得られた値など（ランダムでなければ意味がない）
• 集団にはばらつきがあるので毎回異なる値が得られる
• →ばらつきを考慮して母集団の性質を推定する

• 例えばこんなとき…
• とある卒研生が「栄養豊富な餌で育ったハエは体が大きくなる」ことを主張しようとしてデータを集めた。
• これまでのデータによると、通常の餌で育てたハエの体長は平均3.0mm, 標準偏差1.0mmの正規分布に従う。
• 卒研生が栄養豊富な餌で育てたハエ10匹の体長は、3.0, 3.0, 3.2, 3.4, 3.6, 4.0, 4.2, 4.2, 4.3, 4.5 mmであった。
• この結果から、卒研生は栄養豊富な餌で育ったハエは身体が大きくなると結論づけた。
• ところが教授はこれに対して「たまたま大きいハエがとれちゃったんじゃないの？」とコメントした。
• さて、この教授にどのように反論したらよいだろうか？

「こんなことがたまたま起こる確率はすごく低いです！」

• 母集団からこのような標本が得られる可能性が低いことを示す
  

帰無仮説（通常餌の母集団からこの標本が偶然得られた）

対立仮説（偶然ではない＝異なる母集団から得られた）

※帰無仮説と対立仮説は排他的

1. 帰無仮説のもとで今回得られた標本が偶然生じる確率（\(p\)値, \(p\)-value）を計算する
2. \(p\)値が有意水準（\(\alpha\)）より低い場合、帰無仮説を棄却する
   • 伝統的に\(p\) < 0.05で棄却（偶然起こるのは1/20回以下）
3. その結果、対立仮説を採択する（=「有意差がある」）

\(p\)値は検定統計量に基づいて求める

• 検定統計量とは…
  • 仮説検定で用いられる統計量
  • （めっちゃざっくり言うと、とある前提に基づいて標本の性質をまとめた仮説検定の基準になる値）
  • 標本から計算された値を「検定統計量の実現値」と呼ぶ
  • \(Z\)統計量、\(t\)統計量、\(F\)統計量、カイ二乗統計量など
• 帰無仮説のもとでの検定統計量の確率分布を元に、「得られた検定統計量の実現値が偶然得られる確率（=\(p\)値）」を計算する
• \(p\)値が有意水準（\(\alpha=0.05\)）より低ければ帰無仮説を棄却する

• 確率分布とは…ある確率変数がどんな確率でどんな値をとるかを表した分布（Xが値でYが確率）
• 確率変数とは…実際に結果が得られるまでどんな値が得られるかが決まっていない変数
  • 同じ手続きでデータを得ても異なる値が得られるもの = 多くの実験／観測データはこれに当てはまる
• 確率の総和は１となる
• さまざまな典型的な確率分布が知られる

仮説検定の手続き（3~5はRが勝手にやってくれる）

1. 母集団に関する帰無仮説と対立仮説を設定する
2. 検定統計量（=検定方法）を選ぶ
   • 検定の目的と標本の性質によって変わる
   • \(Z\)統計量、\(t\)統計量、\(F\)統計量、カイ二乗統計量など
3. 有意水準\(\alpha\)を決める（伝統的には\(\alpha = 0.05\)）
4. 標本から検定統計量の実現値を求める
5. 帰無仮説のもとでの検定統計量の確率分布と、検定統計量の実現値を比較し、「帰無仮説のもとで得られた検定統計量の実現値が偶然得られる確率（=\(p\)値）」を計算する
   
6. \(p\)値が有意水準より低ければ帰無仮説を棄却する

• とある卒研生（p.6）の例だと…母集団は正規分布に従い、平均（=3.0）と 標準偏差（=1.0）がわかっている
• 平均と標準偏差が既知の正規分布の場合、\(Z\)統計量が使える
  • \(Z = \frac{\bar{X} - \mu}{\sqrt{\sigma^2/n}}\)…平均値の差を標準誤差\({\sqrt{\sigma^2/n}}\)で標準化
    • \(\bar{X}\)…標本の平均 = 3.74
    • \(\mu\)…母集団の平均 = 3.0
    • \(\sigma\)…母集団の標準偏差 = 1.0
    • \(n\)…サンプルサイズ = 10
• 帰無仮説のもとでは\(Z\)は標準正規分布（平均0, 標準偏差１の正規分布）に従う
• 今回の場合、\(Z = \frac{3.74 - 3}{\sqrt{1^2/10}}\) = 2.340085

• 帰無仮説のもとで\(Z\)が従う標準正規分布では、\(Z\)が灰色の範囲（-1.96 < \(Z\) < 1.96）外の値をとる確率は5%（=有意水準\(\alpha\)）

• 今回の場合、\(Z=2.340085\) ←範囲外！
• 帰無仮説のもとで\(Z=2.340085\)になる確率（=\(p\)値）は0.01927935
• → 有意水準\(\alpha=0.05\)より低い
• → 帰無仮説を棄却し、対立仮説を採用する

標本の性質や検定の目的によって使う検定統計量は異なる

• 母集団が平均と分散が既知の正規分布である場合…

  • \(Z\)統計量：\(\frac{\bar{X} - \mu}{\sqrt{\sigma^2/n}}\)…平均値の差を標準誤差\({\sqrt{\sigma^2/n}}\)で標準化
  • 帰無仮説のもとでは\(Z\)は標準正規分布に従う

• 母集団が平均が既知、分散が未知の正規分布である場合…

  • \(t\)統計量：\(\frac{\bar{X} - \mu}{\sqrt{\hat{\sigma}^2/n}}\)…母分散\(\sigma^2\)の代わりに不偏分散\(\hat{\sigma}^2\)を使う
  • 帰無仮説のもとでは\(t\)は自由度\(df = n-1\)の\(t\)分布に従う

• 他にも\(F\)統計量やカイ二乗統計量など
  

• 不適切な統計量（=方法）を用いると誤った\(p\)値が得られる

統計解析法にはそれぞれ守るべき前提条件がある

• 正しい\(p\)値を求めるために必要
• 標本の性質や解析の目的にあった方法を使わないと間違った\(p\)値が得られてしまう

有意差を求めて間違った解析法を使うのは不正／不誠実

• 間違った方法によって得られた\(p < 0.05\)に意味はない

自分のデータに合った解析を選べるようになろう！

• 今回は古典的な統計的仮説検定→統計モデリングの入口のみ
• より良い解析法を常に検討していく姿勢が大切！
  • より複雑なモデル、ベイズ統計など

\(p\)>0.05 →「差がない」と結論するのは間違い

• \(p\)>0.05 → 帰無仮説が棄却できない ≠ 差がない
• 統計的仮説検定の立場からは「どちらとも言えない」
• 態度を保留するのが正解

\(p\)値が小さい →「差が大きい」と結論するのも間違い

• \(p\)値はサンプルサイズが大きいと有意になりやすい
• \(p\)値が小さいからといって差が大きいとは限らない
• 差の大きさを示すには効果量（effect size）
  • eagystatsパッケージ群が便利かも（日本語解説）

データの性質とやりたいことによって方法は変わる

penguinsで練習しよう

【復習】データを読み込んでざっくり眺める

library(palmerpenguins)               #penguinsを読み込み
library(tidyverse)                    #tidyverseを読み込み
head(penguins)                        #penguinsの最初を見せて！

## # A tibble: 6 x 8
##   species island bill_length_mm bill_depth_mm flipper_length_… body_mass_g sex  
##   <fct>   <fct>           <dbl>         <dbl>            <int>       <int> <fct>
## 1 Adelie  Torge…           39.1          18.7              181        3750 male 
## 2 Adelie  Torge…           39.5          17.4              186        3800 fema…
## 3 Adelie  Torge…           40.3          18                195        3250 fema…
## 4 Adelie  Torge…           NA            NA                 NA          NA <NA> 
## 5 Adelie  Torge…           36.7          19.3              193        3450 fema…
## 6 Adelie  Torge…           39.3          20.6              190        3650 male 
## # … with 1 more variable: year <int>

• アデリーペンギンの体重に性差があるか？

アデリーペンギンの体重に性差があるか？

[練習問題]

• まずはデータをプロットしよう
  • 元データはpenguins
  • dplyrのfilterでspecies == “Adelie”だけ抽出
  • ggplot2でプロット
    • X軸…sex
    • Y軸…body_mass_g

アデリーペンギンの体重に性差があるか？

penguins_adelie = penguins %>%
  filter(species == "Adelie")
head(penguins_adelie)

## # A tibble: 6 x 8
##   species island bill_length_mm bill_depth_mm flipper_length_… body_mass_g sex  
##   <fct>   <fct>           <dbl>         <dbl>            <int>       <int> <fct>
## 1 Adelie  Torge…           39.1          18.7              181        3750 male 
## 2 Adelie  Torge…           39.5          17.4              186        3800 fema…
## 3 Adelie  Torge…           40.3          18                195        3250 fema…
## 4 Adelie  Torge…           NA            NA                 NA          NA <NA> 
## 5 Adelie  Torge…           36.7          19.3              193        3450 fema…
## 6 Adelie  Torge…           39.3          20.6              190        3650 male 
## # … with 1 more variable: year <int>

アデリーペンギンの体重に性差があるか？

gp = ggplot(data = penguins_adelie) +
  geom_point(aes(x = sex, y = body_mass_g), 
             position = position_jitter(width = 0.05))
gp

## Warning: Removed 1 rows containing missing values (geom_point).

• オスのほうが大きそう…！でもNAとかあるなぁ…

アデリーペンギンの体重に性差があるか？

penguins_adelie = penguins %>%
  filter(species == "Adelie", !is.na(sex)) #NAを除く
head(penguins_adelie)

## # A tibble: 6 x 8
##   species island bill_length_mm bill_depth_mm flipper_length_… body_mass_g sex  
##   <fct>   <fct>           <dbl>         <dbl>            <int>       <int> <fct>
## 1 Adelie  Torge…           39.1          18.7              181        3750 male 
## 2 Adelie  Torge…           39.5          17.4              186        3800 fema…
## 3 Adelie  Torge…           40.3          18                195        3250 fema…
## 4 Adelie  Torge…           36.7          19.3              193        3450 fema…
## 5 Adelie  Torge…           39.3          20.6              190        3650 male 
## 6 Adelie  Torge…           38.9          17.8              181        3625 fema…
## # … with 1 more variable: year <int>

アデリーペンギンの体重に性差があるか？

gp = ggplot(data = penguins_adelie) +
  geom_point(aes(x = sex, y = body_mass_g), 
             position = position_jitter(width = 0.05))
gp

• いい感じ！さて…

データの正規性と等分散性によって使える方法は変わる

正規分布とは

• 左右対象の釣鐘型の分布
• 現実世界でしばしば見られる
  • ある一つの数値を目標とした作業で生じる偶然的な誤差
  • 性別と年齢を固定したときの身長の分布平均と分散
• 平均と分散（または標準偏差）がわかればどのような分布になるか一意に決まる（めちゃ便利）

• この場合、オスのほうがメスより分散が大きい
• 実際はFテストやBartlettテストの結果で判断する

統計的仮説検定の進め方

1. データをプロットして眺める
2. 各標本に正規性があるか調べる
   • Q-Q plot
   • Shapiro-Wilkテスト
3. 等分散性はあるか調べる
   • Fテスト
4. 2, 3の結果を受けて検定方法を決め、検定する
   • 正規性/等分散性の有無で使える方法が違う
   • 各検定方法の前提条件をよく確認すること

1. 各標本に正規性があるか（Q-Q plot）

gp = ggplot(data = penguins_adelie) +
       stat_qq(aes(sample = body_mass_g, color = sex)) + 
       facet_wrap( ~ sex, scales = "free")
gp

• 正規Q-Q plotで直線上に乗っているような気がする

1. 各標本に正規性があるか

• Shapiro-Wilkテスト
  • shapiro.test(【調べたい標本】)
    • 【調べたい標本】はベクトルc(a, b, c…)で入れる
    • 【data.frame】$【列名】でも指定できる
  • 帰無仮説：正規性がある
  • p<0.05で正規性がないことを示す
  • （正規性があることは言えない）
  • １標本の値を入れる（２標本を混ぜない）

1. 各標本に正規性があるか（Shapiro-Wilkテスト）

sw_test_results = penguins_adelie %>%   #penguins_adelieを使う
  group_by(sex) %>%                     #sexでグループ
  summarise(statistic = shapiro.test(body_mass_g)$statistic, 
        #body_mass_gにshapiro.testを行い、そのstatistic値をstatisticという列に
            p.value = shapiro.test(body_mass_g)$p.value,    #同様
            .groups     = "drop") #グループを解除
head(sw_test_results)

## # A tibble: 2 x 3
##   sex    statistic p.value
##   <fct>      <dbl>   <dbl>
## 1 female     0.977   0.199
## 2 male       0.983   0.416

• 正規性がないとは言えない→「正規性あり」と判断

2. 等分散性があるか

• Fテスト
  • ベクトルとして
    • var.test(【標本A】, 【標本B】)
      • 標本はベクトルc(a, b, c…)で入れる
  • データフレームとして
    • var.test(data = 【data.frame】, 【調べたい値の列名】~ 【グループ分けの列名】)
  • 帰無仮説：等分散性がある
  • p<0.05で等分散性がないことを示す

2. 等分散性があるか（Fテスト）

var.test(data = penguins_adelie, body_mass_g ~ sex)

## 
##  F test to compare two variances
## 
## data:  body_mass_g by sex
## F = 0.60331, num df = 72, denom df = 72, p-value = 0.03356
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
##  0.3787186 0.9611059
## sample estimates:
## ratio of variances 
##          0.6033147

• p<0.05なので「等分散性なし」と判断

アデリーペンギンの体重に性差があるか？

• 正規性はあり
• 等分散性はなし
• 普通のt検定（正規性と等分散性が前提条件）は使えない
• → Welchのt検定（正規性のみが前提条件）を使う
  • フローチャートを参照

正規性あり等分散なしの２群の検定

• Welchのt検定
  • ベクトルとして
    • t.test(【標本A】, 【標本B】)
      
  • データフレームとして
    • t.test(data = 【data.frame】, 【調べたい値の列名】~ 【グループ分けの列名】)
      
  • 帰無仮説：平均が等しい
    
  • p<0.05で平均が異なる母集団に由来することを示す

アデリーペンギンの体重に性差があるか？(Welchのt検定)

t.test(data = penguins_adelie, body_mass_g ~ sex)

## 
##  Welch Two Sample t-test
## 
## data:  body_mass_g by sex
## t = -13.126, df = 135.69, p-value < 2.2e-16
## alternative hypothesis: true difference in means between group female and group male is not equal to 0
## 95 percent confidence interval:
##  -776.3012 -573.0139
## sample estimates:
## mean in group female   mean in group male 
##             3368.836             4043.493

• 帰無仮説「平均が等しい」は棄却→有意差あり

アデリーペンギンの体重に性差があるか？(Welchのt検定)

gp = ggplot(data = penguins_adelie) +
  geom_point(aes(x = sex, y = body_mass_g), size = 0.8,
             position = position_jitter(width = 0.07), alpha = 0.5) +
  annotate("text", x = 1.5, y = 5200, label = "***", size = 5, color = "gray30") +
  annotate("segment", x = 1.2, xend = 1.8, y = 5000, yend = 5000, color = "gray30") +
  coord_cartesian(ylim = c(0, 6000))
gp

ようやくグラフが完成！

アデリーペンギンの体重に性差があるか？(Welchのt検定)

• 結果をcsvで出力したいときはeasystatsパッケージを使う
  • パッケージをインストールしてから…
  • report(【統計解析】)
    • このままだと文章型で出力される
  • 後ろに%>% as.data.frameとすると表型になる
  • さらに後ろに%>% write_csvで書き出せる

var.equal = の設定で等分散性ありの検定に変えられる

等分散性なし→Welchのt検定

• t.test(data, Y ~ X, var.equal = FALSE)…デフォルト
  • 何も設定しなかったらこっち

等分散性あり→Studentのt検定

• t.test(data, Y ~ X, var.equal = TRUE)

等分散性がわからない時点で、F検定をせずにWelchのt検定をすべきという考え方がメジャーになりつつある

paired = の設定で対応ありの検定に変えられる

対応なし

• t.test(data, Y ~ X, paired = FALSE)…デフォルト

対応あり

• t.test(data, Y ~ X, paired = TRUE)
  • 同じ個体から複数回とったデータを比較したいとき

［練習問題］

• 対応なし、等分散性ありの検定をしてみよう
• 対応あり、等分散性なしの検定をしてみよう

［練習問題］

• 対応なし、等分散性ありの検定をしてみよう

t.test(data = penguins_adelie, body_mass_g ~ sex, 
       paired = FALSE, var.equal = TRUE) # paired = FALSEは省略可能

## 
##  Two Sample t-test
## 
## data:  body_mass_g by sex
## t = -13.126, df = 144, p-value < 2.2e-16
## alternative hypothesis: true difference in means between group female and group male is not equal to 0
## 95 percent confidence interval:
##  -776.2484 -573.0666
## sample estimates:
## mean in group female   mean in group male 
##             3368.836             4043.493

［練習問題］

• 対応あり、等分散性なしの検定をしてみよう

t.test(data = penguins_adelie, body_mass_g ~ sex, 
       paired = TRUE, var.equal = FALSE) # var.equal = FALSEは省略可能

## 
##  Paired t-test
## 
## data:  body_mass_g by sex
## t = -14.264, df = 72, p-value < 2.2e-16
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -768.944 -580.371
## sample estimates:
## mean of the differences 
##               -674.6575

くちばしの形は雌雄で異なるか？

• 細長さは(bill_length_mm)÷(bill_depth_mm)で指標が作れそう
• こういう割り算データは正規性がないと思ったほうがいい
• （平均値や中央値が0や1に近いときの分布を考えてみよう）

くちばしの細長さは雌雄で異なるか？

[練習問題]

• アデリーペンギンのくちばしの細長さを計算しよう
• 計算できたらプロットしてみよう

くちばしの細長さは雌雄で異なるか？

[練習問題]

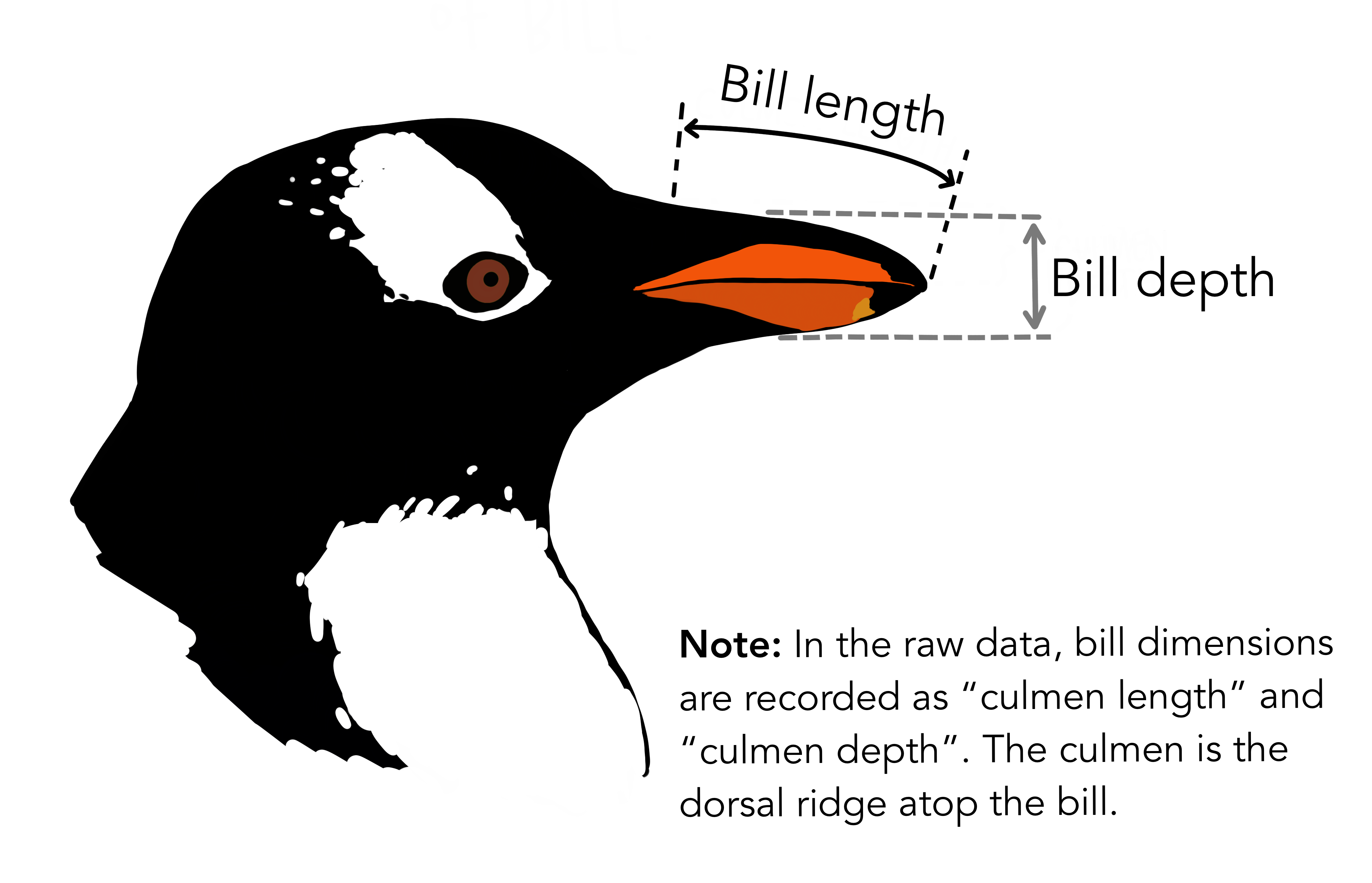
penguins_adelie = penguins %>%
  filter(species == "Adelie", !is.na(sex)) %>% #NAを除く
  mutate(ratio = bill_depth_mm/bill_length_mm)
head(penguins_adelie)

## # A tibble: 6 x 9
##   species island bill_length_mm bill_depth_mm flipper_length_… body_mass_g sex  
##   <fct>   <fct>           <dbl>         <dbl>            <int>       <int> <fct>
## 1 Adelie  Torge…           39.1          18.7              181        3750 male 
## 2 Adelie  Torge…           39.5          17.4              186        3800 fema…
## 3 Adelie  Torge…           40.3          18                195        3250 fema…
## 4 Adelie  Torge…           36.7          19.3              193        3450 fema…
## 5 Adelie  Torge…           39.3          20.6              190        3650 male 
## 6 Adelie  Torge…           38.9          17.8              181        3625 fema…
## # … with 2 more variables: year <int>, ratio <dbl>

くちばしの細長さは雌雄で異なるか？

[練習問題]

gp = ggplot(data = penguins_adelie) +
  geom_point(aes(x = sex, y = ratio), 
             position = position_jitter(width = 0.05))
gp

くちばしの細長さは雌雄で異なるか？

1. 各標本に正規性はあるか（Q-Q plot）

gp = ggplot(data = penguins_adelie) +
       stat_qq(aes(sample = ratio, color = sex)) + 
       facet_wrap( ~ sex, scales = "free")
gp

くちばしの細長さは雌雄で異なるか？

1. 各標本に正規性はあるか（Shapiro-Wilkテスト）

sw_test_results = penguins_adelie %>%   #penguins_adelieを使う
  group_by(sex) %>%                     #sexでグループ
  summarise(statistic = shapiro.test(ratio)$statistic, 
            p.value = shapiro.test(ratio)$p.value, 
            .groups     = "drop") 
head(sw_test_results)

## # A tibble: 2 x 3
##   sex    statistic p.value
##   <fct>      <dbl>   <dbl>
## 1 female     0.975 0.164  
## 2 male       0.954 0.00962

くちばしの細長さは雌雄で異なるか？

2. 等分散性があるか（Fテスト）

var.test(data = penguins_adelie, ratio ~ sex)

## 
##  F test to compare two variances
## 
## data:  ratio by sex
## F = 0.73443, num df = 72, denom df = 72, p-value = 0.1928
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
##  0.4610261 1.1699847
## sample estimates:
## ratio of variances 
##          0.7344341

くちばしの細長さは雌雄で異なるか？

• 正規性はなし
• 等分散性はあり
• 対応はない
• → Wilcoxonの順位和検定（U検定と同じ）を行う
  • フローチャートを参照

正規性なし等分散性ありの２群の比較

• Wilcoxonの順位和検定
  • デフォルトのwilcox.test()ではタイ（同値）があった場合に正確なp値が出ないのでcoinパッケージを使う
    • ベクトルとして
      • wilcox_test(【標本A】, 【標本B】, distribution = “exact”)
        
    • データフレームとして
      • wilcox_test(data = 【data.frame】, 【調べたい値の列名】~ 【グループ分けの列名】, distribution = “exact”)
        
  • 帰無仮説：２群間に差がない
    
  • p<0.05で異なる母集団に由来することを示す

くちばしの細長さは雌雄で異なるか？

まずインストールする（１行目の#を消して走らせる）

#install.packages("coin")
library(coin)             # 読み込み
wilcox_test(data = penguins_adelie, ratio ~ sex, distribution = "exact")

## 
##  Exact Wilcoxon-Mann-Whitney Test
## 
## data:  ratio by sex (female, male)
## Z = 0.29941, p-value = 0.7661
## alternative hypothesis: true mu is not equal to 0

• 帰無仮説「２群間に差がない」は棄却されない→有意差なし

対応なし→Wilcoxonの順位和検定

• wilcox_test(data, Y ~ X, distribution = “exact”)

対応あり→Wilcoxonの符号順位検定

• wilcoxsign_test(data, Y ~ X, distribution = “exact”)

• Brunner-Munzel検定

• Brunner-Munzel検定
  • brunnermunzelパッケージを使う
  • ベクトルとして
    • brunnermunzel.test(【標本A】, 【標本B】)
      
  • データフレームとして
    • brunnermunzel.test(data = 【data.frame】, 【調べたい値の列名】~ 【グループ分けの列名】)
      
  • 帰無仮説：２群間に差がない
  • p<0.05で異なる母集団に由来することを示す
    
  • 「サンプル数が少ない」というエラーが出たらbrunnermunzel.permutation.test

さっきのデータで使ってみよう

まずインストールする（１行目の#を消して走らせる）

#install.packages("brunnermunzel")
library(brunnermunzel)             # 読み込み
brunnermunzel.test(data = penguins_adelie, ratio ~ sex)

## 
##  Brunner-Munzel Test
## 
## data:  ratio by sex
## Brunner-Munzel Test Statistic = -0.29701, df = 143.58, p-value = 0.7669
## 95 percent confidence interval:
##  0.3901081 0.5811811
## sample estimates:
## P(X<Y)+.5*P(X=Y) 
##        0.4856446

1. まずはプロット
2. 正規性, 等分散性, 対応あり/なしを確認
   • Q-Q plot, Shapiro-Wilkテスト
   • F検定
3. 検定方法を決める
   • Studentのt検定（対応あり／なし）
   • Welchのt検定（対応あり／なし）
   • Wilcoxonの順位和検定
   • Wilcoxonの符号順位検定
   • Brunner-Munzel検定（対応あり／なし）

２群の比較を単に繰り返すのはダメ

• 仮説検定の考え方を思い出そう

1. 同じ母集団由来であった場合に今回得られた標本の差が生じる確率が低い（<5%）→帰無仮説を棄却する
2. その結果、対立仮説を採用する

どこかで有意差が出る確率はどんどん高まる

• 100回検定すれば5回は偶然有意差が出る 阪大医学・老年・腎臓内科学HP

有意差があった群のみ検定したことにする？

→もちろん不正！！

多重比較法を使うか、有意水準を補正する

• 今回は多重比較を紹介します
• 有意水準の補正の方法はこちらなど

【復習】読み込んでデータをざっくり眺める

library(palmerpenguins)               #penguinsを読み込み
library(tidyverse)                    #tidyverseを読み込み
head(penguins)                        #penguinsの最初を見せて！

## # A tibble: 6 x 8
##   species island bill_length_mm bill_depth_mm flipper_length_… body_mass_g sex  
##   <fct>   <fct>           <dbl>         <dbl>            <int>       <int> <fct>
## 1 Adelie  Torge…           39.1          18.7              181        3750 male 
## 2 Adelie  Torge…           39.5          17.4              186        3800 fema…
## 3 Adelie  Torge…           40.3          18                195        3250 fema…
## 4 Adelie  Torge…           NA            NA                 NA          NA <NA> 
## 5 Adelie  Torge…           36.7          19.3              193        3450 fema…
## 6 Adelie  Torge…           39.3          20.6              190        3650 male 
## # … with 1 more variable: year <int>

• ペンギンの体重は種ごとに異なるか？

ペンギンの体重は種ごとに異なるか？

• 体重に性差があるのでメスに限定して調べよう
• まずはデータをプロットしよう

penguins_female = penguins %>%
  filter(sex == "female")
head(penguins_female)

## # A tibble: 6 x 8
##   species island bill_length_mm bill_depth_mm flipper_length_… body_mass_g sex  
##   <fct>   <fct>           <dbl>         <dbl>            <int>       <int> <fct>
## 1 Adelie  Torge…           39.5          17.4              186        3800 fema…
## 2 Adelie  Torge…           40.3          18                195        3250 fema…
## 3 Adelie  Torge…           36.7          19.3              193        3450 fema…
## 4 Adelie  Torge…           38.9          17.8              181        3625 fema…
## 5 Adelie  Torge…           41.1          17.6              182        3200 fema…
## 6 Adelie  Torge…           36.6          17.8              185        3700 fema…
## # … with 1 more variable: year <int>

ペンギンの体重は種ごとに異なるか？

• まずはデータをプロットしよう

gp = ggplot(data = penguins_female) +
  geom_point(aes(x = species, y = body_mass_g), 
             position = position_jitter(width = 0.05))
gp

• 差がありそうな雰囲気…！

３群以上の比較を行うときも進め方は同じ

1. データをプロットして眺める
2. 各標本に正規性があるか調べる
   • Q-Q plot
   • Shapiro-Wilkテスト
3. 等分散性はあるか調べる
   • Bartlettテスト ←Fテストの多群版
4. 2, 3の結果を受けて検定方法を決め、検定する

1. 各標本に正規性はあるか（Q-Q plot）

gp = ggplot(data = penguins_female) +
  stat_qq(aes(sample = body_mass_g, color = species)) + 
  facet_wrap( ~ species, scales = "free")
gp

• 正規Q-Q plotで直線上に乗っているような気がする

1. 各標本に正規性はあるか（Shapiro-Wilkテスト）

sw_test_results = penguins_female %>%   #penguins_adelieを使う
  group_by(species) %>%                     #speciesでグループ
  summarise(statistic = shapiro.test(body_mass_g)$statistic, 
        #body_mass_gにshapiro.testを行い、そのstatistic値をstatisticという列に
            p.value = shapiro.test(body_mass_g)$p.value,    #同様
            .groups     = "drop") #グループを解除
head(sw_test_results)

## # A tibble: 3 x 3
##   species   statistic p.value
##   <fct>         <dbl>   <dbl>
## 1 Adelie        0.977   0.199
## 2 Chinstrap     0.963   0.306
## 3 Gentoo        0.981   0.511

• 「正規性あり」と判断

2. 等分散性があるか

• Bartlettテスト
  • ベクトルとして
    • bartlett.test(x = list(A, B, C))
  • データフレームとして
    • bartlett.test(data = 【data.frame】, 【調べたい値の列名】~ 【グループ分けの列名】)
  • 帰無仮説：等分散性がある
  • p<0.05で等分散性がないことを示す

2. 等分散性があるか（Bartlettテスト）

bartlett.test(data = penguins_female, body_mass_g ~ species)

## 
##  Bartlett test of homogeneity of variances
## 
## data:  body_mass_g by species
## Bartlett's K-squared = 0.19828, df = 2, p-value = 0.9056

• 「等分散性あり」と判断

ペンギンの体重は種ごとに異なるか？

• 正規性あり
• 等分散性あり
• ３群以上
• → 一元分散分析（ANOVA）を使う

正規性あり等分散性ありの多群比較

• 一元分散分析（ANOVA）
  • summary(aov(data = 【data.frame】, 【調べたい値の列名】~ 【グループ分けの列名】))
    
  • 帰無仮説：全ての群が同一の母集団に由来する（=全ての群に差がない）
  • p<0.05で異なる母集団に由来することを示す

ペンギンの体重は種ごとに異なるか？

summary(aov(data = penguins_female, body_mass_g ~ species))

##              Df   Sum Sq  Mean Sq F value Pr(>F)    
## species       2 60350016 30175008   393.2 <2e-16 ***
## Residuals   162 12430757    76733                   
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

• 有意差はある
• 帰無仮説（群間に差がない）は棄却された
• どのペアに差があるのか？
  • post-hocテストを行う

正規性あり等分散性ありの多群比較のpost-hocテスト

• Tukeyの多重比較
  • TukeyHSD(aov(data = 【data.frame】, 【調べたい値の列名】~ 【グループ分けの列名】))
    
  • 帰無仮説：２群間に差がない
    
  • p<0.05で異なる母集団に由来することを示す

ペンギンの体重は種ごとに異なるか？

TukeyHSD(aov(data = penguins_female, body_mass_g ~ species))

##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = body_mass_g ~ species, data = penguins_female)
## 
## $species
##                       diff        lwr       upr     p adj
## Chinstrap-Adelie  158.3703   22.32078  294.4197 0.0179471
## Gentoo-Adelie    1310.9058 1195.64908 1426.1624 0.0000000
## Gentoo-Chinstrap 1152.5355 1011.00620 1294.0648 0.0000000

ペンギンの体重は種ごとに異なるか？

gp = ggplot(data = penguins) +
  geom_point(aes(x = species, y = body_mass_g), size = 0.5, 
             position = position_jitter(width = 0.05), alpha = 0.3) +
  annotate("text", x = c(1, 2, 3), y = 7000, label = c("a", "b", "c")) +
  coord_cartesian(ylim = c(0, 8000))
gp

## Warning: Removed 2 rows containing missing values (geom_point).

できあがり！

正規性なし、等分散性ありの場合は…

• Kruscal-Wallis検定
  • kruskal.test(data = 【data.frame】, 【調べたい値の列名】~ 【グループ分けの列名】)
    
  • 帰無仮説：全ての群に差がない
    
  • p<0.05で異なる母集団に由来することを示す
    
  • ただし近似のp値を計算するのでサンプルサイズが小さい場合は注意

post-hocは…

• Steel-Dwass検定
  • NSM3パッケージを使う
  • pSDCFlig(【調べたい値をベクトルで】, 【グループ分けをベクトルで】, method = 【方法】)
    • methodは３種類
      • “Exact”…正確
      • “Asymptotic”… 漸近
      • “Monte Carlo”…モンテカルロ法
        • 正確以外の場合はサンプルサイズに注意
  • 帰無仮説：２群間に差がない
    
  • p<0.05で異なる母集団に由来することを示す

ペンギンの体重は種ごとに異なるか？（Kruscal-Wallis）

kruskal.test(data = penguins_female, body_mass_g ~ species)

## 
##  Kruskal-Wallis rank sum test
## 
## data:  body_mass_g by species
## Kruskal-Wallis chi-squared = 115.24, df = 2, p-value < 2.2e-16

1. まずはプロット
2. 正規性, 等分散性, 対応あり/なしを確認
   • Q-Q plot, Shapiro-Wilkテスト
   • Bartlettテスト
3. 検定方法を決める
   • ANOVA → Tukey
   • Kruscal-Wallis → Steel-Dwass
   • フローチャートを参照

２要因の場合は…

• Two-way ANOVAやFriedman検定など

ペンギンの性比は種ごとに異なるか？

penguins_sexratio_sum = penguins %>% 
  group_by(species, sex) %>%            # speciesとsexごとにグループ分け
  summarise(length = length(species),   # N数を数える
            .groups     = "drop") %>%   # groupを解除
  filter(!is.na(sex)) %>%               # sex == NAを除去
  print()                               # 表示

## # A tibble: 6 x 3
##   species   sex    length
##   <fct>     <fct>   <int>
## 1 Adelie    female     73
## 2 Adelie    male       73
## 3 Chinstrap female     34
## 4 Chinstrap male       34
## 5 Gentoo    female     58
## 6 Gentoo    male       61

ペンギンの性比は種ごとに異なるか？

gp = ggplot(data = penguins_sexratio_sum, aes(x = species, y = length)) +
  geom_bar(aes(fill = sex), stat = "identity", position = "fill") +
  scale_y_continuous(labels = scales::percent) +
  coord_flip()                    # X軸とY軸を逆にする
gp

• まぁ違わなそうですけどね…

• カイ２乗検定
  • chisq.test(【ベクトルA】,【ベクトルB】)
    • A…【data.frame】$【調べたい値の列名】
    • B…【data.frame】$【グループ分けの列名】
  • 帰無仮説：２群の比率に差がない
    
  • サンプル数が小さい場合はフィッシャーの正確確率検定
• フィッシャーの正確確率検定
  • fisher.test(【ベクトルA】,【ベクトルB】)
    • A…【data.frame】$【調べたい値の列名】
    • B…【data.frame】$【グループ分けの列名】
  • 帰無仮説：２群の比率に差がない

ペンギンの性比は種ごとに異なるか？

penguins_sexratio = penguins %>%
  filter(!is.na(sex))              # NAを除く
chisq.test(penguins_sexratio$sex, penguins_sexratio$species)

## 
##  Pearson's Chi-squared test
## 
## data:  penguins_sexratio$sex and penguins_sexratio$species
## X-squared = 0.048607, df = 2, p-value = 0.976

統計的仮説検定は古くから用いられている方法

だけどこれだとうまく解析できないことも…

• 例えば値と値の関係性とか、複数の要因が考えられるとき
  
  

→こういうときは統計モデリングが適している

応答変数と説明変数

• 応答変数（目的変数／従属変数; Y）：調べたい値
• 説明変数（独立変数; X）：Yのばらつきの要因として調べる変数

一般線形モデル（Linear model, LM）

• 説明変数と応答変数を線形回帰するモデリング手法
• 前提：応答変数の残差は正規分布に従う

一般化線形モデル（Generalized linear model, GLM）

• 線形以外の式（制限あり）にも回帰できるモデリング手法
• 前提：応答変数の残差は正規分布、二項分布、ポアソン分布などに従う

【復習】データを読み込んでざっくり眺める

library(palmerpenguins)               #penguinsを読み込み
library(tidyverse)                    #tidyverseを読み込み
head(penguins)                        #penguinsの最初を見せて！

## # A tibble: 6 x 8
##   species island bill_length_mm bill_depth_mm flipper_length_… body_mass_g sex  
##   <fct>   <fct>           <dbl>         <dbl>            <int>       <int> <fct>
## 1 Adelie  Torge…           39.1          18.7              181        3750 male 
## 2 Adelie  Torge…           39.5          17.4              186        3800 fema…
## 3 Adelie  Torge…           40.3          18                195        3250 fema…
## 4 Adelie  Torge…           NA            NA                 NA          NA <NA> 
## 5 Adelie  Torge…           36.7          19.3              193        3450 fema…
## 6 Adelie  Torge…           39.3          20.6              190        3650 male 
## # … with 1 more variable: year <int>

• 体重の大きいペンギンは翼長も長い？

体重の大きいペンギンは翼長も長い？

• まずはデータをプロットしよう

gp = ggplot(data = penguins_adelie) +
  geom_point(aes(x = body_mass_g, y = flipper_length_mm)) 
gp

• 微妙な傾向はありそう…統計的にはどうか？

一般線形モデル（Linear model, LM）

• Y ~ β0 + β1X
• 最小二乗法によって残差が最小になるβ0とβ1を求める 　　 引用：biostatics

一般線形モデル（Linear model, LM）

• lm(data =【data.frame】,【応答変数の列名】~【説明変数の列名】)
  • 前提：応答変数の残差は正規分布に従う

体重の大きいペンギンは翼長も長い？（一般線形モデル）

• Coefficients: 回帰係数
  • Estimates: 推定値
    • (Intercept): 切片
    • body_mass_g: body_mass_gの係数
  • Pr(>|t|): 回帰係数が0であるという帰無仮説に対するp値。
    
• （ということは…）
• (Intercept): 1.656e+02 = 165.6
• body_mass_g: 6.610e-03 = 0.00661
• Pr(>|t|): 3.4e-09
• →翼長への体サイズの効果は有意である
• →Y ~ 0.00661X + 165.6に回帰できる

性を考慮したらもう少しうまく説明できるかも…？

複数の説明変数を検討することもできる

• lm(data = 【data.frame】, 【応答変数の列名】~【説明変数１の列名】+【説明変数２の列名】)
  • 前提
    • 応答変数の残差は正規分布に従う
    • 説明変数同士は独立である（相関関係などがない）
  • 有意でない説明変数はモデルから取り除く

　　 引用：久保先生の講義のーと

• 応答変数がマイナス？
  
• 本当にばらつきが一定？（右側でばらつき増えてない？）

一般化線形モデル（Generalized linear model, GLM）

• 一般線形モデル（単回帰、重回帰）を拡張した回帰分析
  • 応答変数の残差は正規分布、二項分布、ポアソン分布などに従う
  • 正規分布にした場合はlm()と同じ
  • lm()を使うより全部glmで解析するのがもはや一般的
    
    
• 誤差構造とリンク関数を設定する
  • 誤差構造：応答変数の残差の確率分布
  • リンク関数：応答変数と説明変数の関係 = 回帰式

一般化線形モデル（Generalized linear model, GLM）

• glm(data = 【data.frame】, 【応答変数】~【説明変数】, family = 【誤差構造】(link = 【リンク関数】))
  • 誤差構造の設定でリンク関数は自動で決まる（変更可能）

ポアソン分布（Poisson distribution）でGLMする

• glm(data = 【data.frame】, 【応答変数の列名】~【説明変数の列名】, family = poisson)

• デフォルトのリンク関数はlog

  • Y ~ exp(β0 + β1X)
  • 指数曲線に回帰される（0 < y < ∞）

• 分散が平均よりかなり大きい場合は負の二項分布を使うが、とりあえずポアソンを試してみることが多い

1. まずはプロット
2. 値の性質から誤差構造とリンク関数を推定する
   • 正規分布, ポアソン分布, 二項分布…
   • 使える分布は他にもある
   • ANOVA的な群間比較も行える（説明変数がfactor型なだけ）
3. 誤差構造とリンク関数を決めてGLMする
4. どのモデルがいちばん“良い”か
   • モデル選択(AICなど)

• 詳しく知りたい人は…統計モデリング概論（Heavy Watal）

必要に応じて複雑なモデリングへ

• “All models are wrong, but some are useful”

1. どんな統計解析ができるか考えてからデータを取ろう
   • 何を統計的に示したいかをはっきりさせる
   • 統計解析しやすい形でデータを取る
     • 連続値？離散値？応答変数？説明変数？
     • 統計解析の前提条件もよく確認する
2. 統計解析に渡しやすい形でデータを取る
   • あるいは元データを変換する（tidyr）
3. まずはプロット！
   • 生データを見ることが一番大切
4. 統計解析する
5. 結果を出力し、考察する